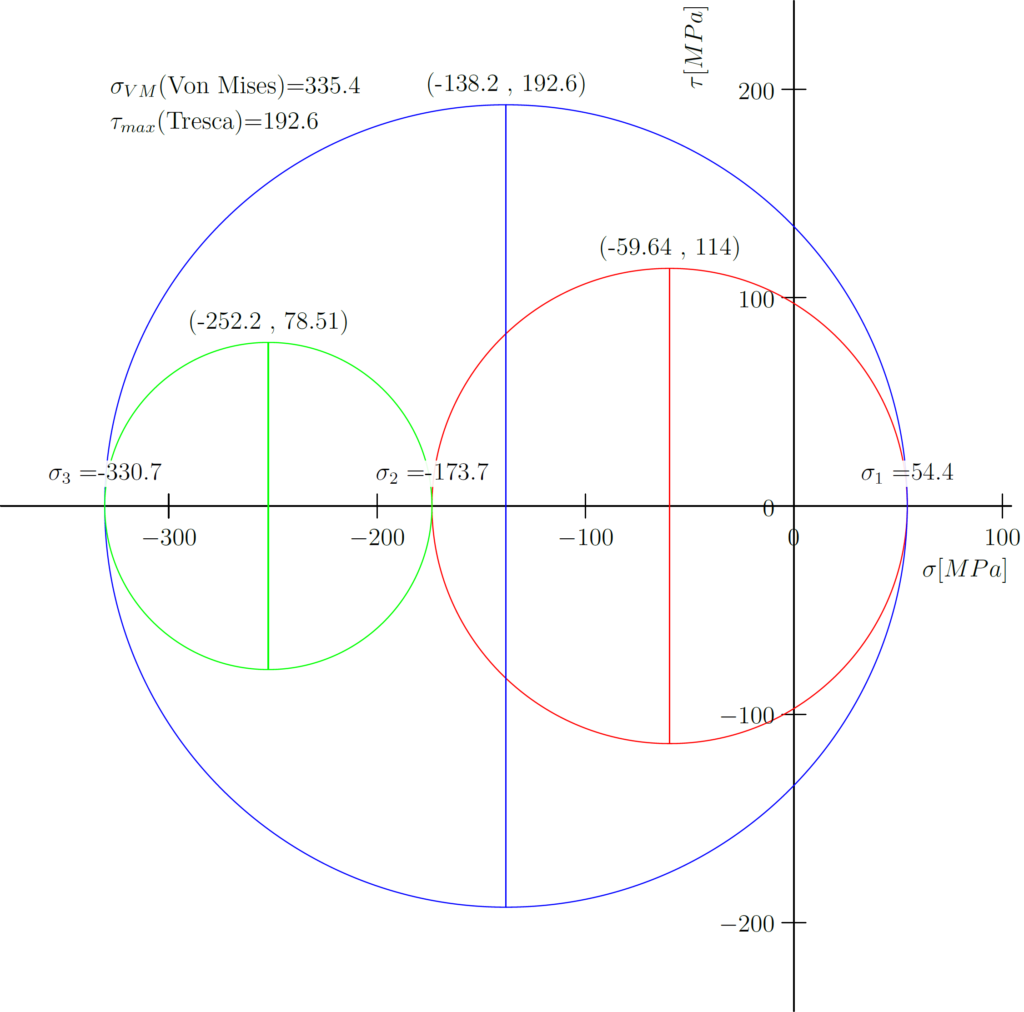
This is an interactive tool for 3D stress analysis. It is made with JavaScript using these libraries:
The source code is included within the HTML.
stress invariants:
$$
\begin{aligned}
I_{1} &=\sigma_{11}+\sigma_{22}+\sigma_{33} \\
I_{2} &=\sigma_{11} \sigma_{22}+\sigma_{22} \sigma_{33}+\sigma_{33}
\sigma_{11}-\sigma_{12}^{2}-\sigma_{23}^{2}-\sigma_{31}^{2} \\
I_{3} &=\sigma_{11} \sigma_{22} \sigma_{33}-\sigma_{11} \sigma_{23}^{2}-\sigma_{22} \sigma_{31}^{2}-\sigma_{33}
\sigma_{12}^{2}+2 \sigma_{12} \sigma_{23} \sigma_{31}
\end{aligned}
$$
$$
\phi=\frac{1}{3} \cos ^{-1}\left(\frac{2 I_{1}^{3}-9 I_{1} I_{2}+27 I_{3}}{2\left(I_{1}^{2}-3 I_{2}\right)^{3 /
2}}\right)
$$
principal stresses in three dimensions:
$$
\begin{aligned}
\sigma_{1} &=\frac{I_{1}}{3}+\frac{2}{3}\left(\sqrt{I_{1}^{2}-3 I_{2}}\right) \cos \phi \\
\sigma_{2} &=\frac{I_{1}}{3}+\frac{2}{3}\left(\sqrt{I_{1}^{2}-3 I_{2}}\right) \cos \left(\phi-\frac{2 \pi}{3}\right)
\\
\sigma_{3} &=\frac{I_{1}}{3}+\frac{2}{3}\left(\sqrt{I_{1}^{2}-3 I_{2}}\right) \cos \left(\phi-\frac{4 \pi}{3}\right)
\end{aligned}
$$